Article Text
Statistics from Altmetric.com
Efforts to measure quality using patient outcomes—whether hospital mortality rates or major complication rates for individual surgery—often become mired in debates over the adequacy of adjustment for case-mix. Some hospitals take care of sicker patients than other hospitals. Some surgeons operate on patients whom other surgeons feel exceed their skill levels. We do not want to penalise hospitals or doctors who accept referrals for more complex patients. Yet, we also do not want to miss opportunities for improvement. Maybe a particular hospital that cares for sicker patients achieves worse outcomes than other hospitals with similar patient populations.
This debate over the adequacy of case-mix adjustment dates back to Florence Nightingale's publication of league tables for mortality in 19th century English hospitals.1 We have made some progress. Some successes have involved supplementing the diagnostic codes and demographic information available in administrative data with a few key clinical variables.2 ,3 Particularly notable successes consist entirely of clinical variables collected for the sole purpose of predicting risk, such as the various prognostic scoring systems for critically ill patients, such as the Acute Physiology and Chronic Health Evaluation and the Simplified Acute Physiology Score4–6 and the National Surgical Quality Improvement Program.7 (Occasionally, research shows that an outcome measure does not require adjustment for case-mix.8)
But, what if comparing mortality rates (or other key patient outcomes) were problematic even with perfect case-mix adjustment? For example, suppose a 75-year-old man undergoing cardiac surgery has diabetes, mild kidney failure and a previous stroke and a 65-year–old woman has hypertension but no previous strokes or kidney problems. Suppose the case-mix adjustment model assigns a risk of death or major complications after surgery of 8% to the 75-year-old man and only 4% to the 65-year-old woman. And, let's say that over time, we see that patients who share the characteristics of the 75-year-old man experience bad outcomes 8% of the time, whereas patients who resemble the 65-year–old woman experience the lower complication rate of 4%. And, let's even add that the model works this well (ie, perfectly) for every type of patient. Having a model like this would seem to put to rest all the debates over the fairness of outcome-based performance measures. Disturbingly, it does not, as first pointed out by Simpson and Yule over 50 years ago.9 ,10
Simpson's paradox
Simpson's paradox (also known as the Yule–Simpson effect)9 ,10 refers to an association or effect found within multiple subgroups but which is reversed when data from these groups are aggregated. One non-technical exposition used batting averages of two prominent professional baseball players as an example (table 1).11 The batting average represents the number of hits divided by the number of ‘at-bats’ (the number of opportunities the player had to hit the ball). In both 1995 and 1996, David Justice had a higher (better) batting average than Derek Jeter. However, aggregating reverses their ranking, with Jeter having the higher batting average in the 2 years combined. This reversal results from the large difference in the number of at-bats between the years, so that the combined average of Jeter was determined most by the 1996 average (which was better than 1995), whereas the opposite was true for Justice. Ross describes how such a pair of players can be found about once a year.11
Illustration of Simpson's paradox using batting averages for two prominent baseball players
Simpson's paradox and risk-adjusted performance measures in healthcare
In this issue, Manktelow et al12 explain how the same phenomenon may occur when comparing standardised mortality ratios (SMRs). Even though two providers have the same mortality risk within subgroups of high-risk and low-risk patients, their overall SMRs differ due to the difference in case-mix of patients that they treat. The authors provide a hypothetical example involving two surgeons (table 2) to illustrate the point before delving into their data-driven analysis of risk-adjusted outcomes across 33 paediatric intensive care units in the UK.
Illustration of Simpson's paradox using the standardised mortality ratio (SMR) for two surgeons with the same observed risk-specific 30-day mortality
As shown in table 2, both surgeons in this example have the same observed and expected mortality rates within subgroups of low-risk and high-risk patients and the same 1.5-fold excess mortality for high-risk patients. However, the overall SMR of Surgeon A is lower (ie, better) than that of Surgeon B. In the baseball example, the change in ranking for the batting averages for the two players occurred because of differences in ‘at-bats’ in the 2 years. With the two hypothetical surgeons in table 2, the change in ranking of their SMRs occurs as a result of differences in case-load across two subgroups of patients, low risk and high risk. The higher overall SMR of Surgeon B reflects the greater proportion of high-risk patients, similar to the difference in at-bats causing the reversal in the baseball example.
Empirical demonstrations of Simpson's paradox are uncommon—one of the reasons the contribution by Manktelow and colleagues is valuable. But, one simulation study of 2×2 tables showed that, given two subgroups of interest and two exposures of interest (eg, Surgeon A vs Surgeon B compared for high-risk and low-risk patients), the apparent effect in the overall group will be the reverse of the effect seen in the subgroups roughly 2% of the time.12a In other words, Surgeon A could achieve a better response than Surgeon B in sicker patients and in low-risk patients, but looking at the aggregate result, Surgeon B would look better than Surgeon A (ie, just as with the baseball example—David Justice had the higher batting average in each of the 2 years, but Derek Jeter has the higher batting average across the 2 years combined). Saying that Simpson's paradox occurs about 2% of the time makes it sound uncommon. But, this frequency refers to the dramatic cases in which the subgroups show the opposite effect as the result seen in the aggregate. Important discrepancies short of complete reversal can still distort the interpretation of clinical research13 and performance measures, such as the widely used hospital standardised mortality ratio (HSMR).14 ,15
Simpson's paradox and SMRs
The HSMR has become as a key measure of hospital quality in various countries.16 ,17 Since its introduction, the HSMR has been heavily criticised on various grounds, including the adequacy of case-mix adjustment using purely administrative data and variations in coding practices.18–20 Often overlooked in this debate is the fact that the HSMR is computed via the indirect standardisation method, so that HSMRs cannot be compared directly across hospitals.21–23
The paper by Manktelow et al12 and a recent paper from Pouw and colleagues24 provide empirical examples of how differences in case-mix can affect the HSMR. These examples highlight the need for caution when hospitals differ in the proportions of high-risk patients that they treat. When such differences exist and the observed mortality risk differs from the expected mortality risk calculated by the HSMR model, Simpson's paradox may rear its head.
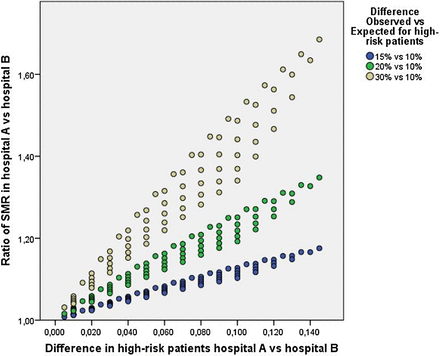
Several variables determine the impact on the HSMR in a situation where both hospitals have equal mortality rates within subgroups of patients. First, the magnitude of the difference between observed and expected mortality matters. If mortality risks are low, say 3% observed versus 1% expected, this excess risk of death will have less impact than would a difference between 30% observed and 10% expected mortality (see the brown dots in figure 1).
The impact of Simpson's paradox on standardised mortality ratio (SMR) for varying differences in case-mix. The graph shows the ratio of the SMR for two hospitals that exhibit the same performance on low-risk and high-risk patients, but the overall SMR is higher for Hospital A due to its higher proportion of high-risk patients. The vertical axis captures this difference by showing the ratio of SMR for Hospital A and Hospital B. The ratio should be 1, but it becomes increasingly higher than 1 with increasing differences between hospitals in the proportion of high-risk patients (shown on the horizontal axis) and with increasing difference between observed and expected mortality (shown in different colours).
Such a dramatic difference may seem unlikely in practice. However, patients directly admitted to intensive care units may exhibit this degree of discrepancy between observed and expected mortality because the severity of their clinical condition is not adequately captured by the variables included in the HSMR model.20 ,25 The HSMR captures comorbid conditions and admitting diagnosis, but cannot capture the severity of the acute illness. For example, two 65-year-old patients with the same chronic illnesses (eg, diabetes, hypertension and mild chronic kidney disease) are admitted to the hospital with pneumonia. They will have the same predicted risk of death, even if one of them has multilobar pneumonia and imminent respiratory failure, requiring admission to the intensive care unit. (Clinical models such as the pneumonia severity index26 and the several widely used scoring systems for predicting outcomes of critical care patients4–6 include variables that do capture disease severity.) Using HSMR data from the Leiden University Medical Centre in 2012, we found that 4.5% of patients were directly admitted to intensive care with an observed mortality risk of 31.4%. Expected mortality based on the Dutch HSMR model was 18.3%. All other patients had an observed mortality of 3.2% compared with 3.4% expected. A difference of 20% observed versus 10% expected (the green dots in the graph) will have less impact. So, the higher the difference between observed and expected mortality, the higher the impact on the HSMR.
A second important factor determining the impact on the HSMR with respect to Simpson's paradox concerns the relative proportions of high-risk patients treated by the hospitals. One might think that small differences in case-mix will exert little impact on the HSMR—for example, if 5% of patients at Hospital A are high-risk while only 1% of Hospital B's patients are high-risk. However, such a small difference in case-mix combined with a considerable excess mortality for these high-risk patients may still have significant impact on the HSMR.
As shown in figure 1, a 5% difference in high-risk patients treated (10% vs 5%) combined with a difference of 30% observed mortality versus 10% expected mortality (the brown dots) results in a 19% higher HSMR (154 vs 130). The same 5% difference and mortality rates have even higher impact if one of the hospitals treats a very small percentage of high-risk patients (eg, 6% vs 1%, resulting in a 27% higher HSMR). This is shown by the ‘bands’ of dots in the same colour in the graph. In these circumstances, the HSMR fails to reflect the fact that mortality risks within subgroups of high-risk and low-risk patients are exactly the same in both hospitals—the HSMR suggests a difference in mortality when, in fact, both hospitals have the same performance. The opposite may also occur. Equivalent HSMRs may mask a higher mortality risk for a group of high-risk patients. So, the impact on the HSMR is determined by the combination of these factors—the magnitude of the difference between observed and expected mortality as well as the difference in the proportions of high-risk patients treated at the hospitals.
What to do about this problem: how can we deal with Simpson's paradox in practice?
Misclassification due to Simpson's paradox relies on disproportionate variations in inputs that produce a performance ranking: (1) the number of observations in a subgroup—whether the number of at-bats in a year or the number of patients in the highest category of risk and (2) the performance within the subgroup (eg, batting average in a year or excess mortality within a high-risk group). When a large imbalance between these inputs exists (due to variations in practice volume, numbers of high-risk patients or coding practices), performance for the aggregate (eg, all patients treated in the hospital) can substantially misrepresent actual performance in subgroups of interest (high-risk and low-risk patients).
Direct comparison of HSMRs between hospitals thus poses problems without additional information on the types of patients treated in different hospitals and does not tell us whether the performance of a hospital for key patient groups (eg, defined by their risk profile from the model or by clinical features not adequately captured in the model, such as direct admission to intensive care) is better than in another hospital. The overall HSMR may be affected by Simpson's paradox, particularly if there are subgroups of patients characterised by high mortality risks and a large difference between observed and expected mortality. This is well known among public health researchers and epidemiologists, who have often pointed out the problems of using the HSMR to produce league tables.13 ,21 ,27
Despite frequent critiques of hospital mortality ratios in the literature,18–20 ,22 ,28 interest in these measures remains high. They are publicly reported in several countries, and various regulatory and commercial organisations will undoubtedly continue to create listings and ranking that use HSMRs in some fashion. Given that HSMRs are here to stay, we need to take appropriate cautions in interpreting them. Publication of HSMRs should be accompanied by descriptions of the types of patients treated at the hospital (eg, the proportions of patients in different risk categories). Publication of HSMRs should probably also be accompanied by a clear message that direct comparisons of HSMRs can be misleading.
The HSMR alone is not sufficient to inform patients or policy makers whether the mortality risk is higher in one hospital or another for a particular group of (high-risk) patients, and thereby support their hospital choice or evaluation of quality of care. Just as we publish warnings for medications, we need to attach cautionary notes to HSMRs. Misinterpretation and misuse of these data will not cause direct harm to patients, but they can cause harm through diverting resources to addressing problems that do not exist and inducing complacency among hospitals that do have problems.
Acknowledgments
The authors thank Drs Chaim Bell, Andrew Auerbach and Saskia le Cessie for their helpful comments on earlier drafts of this manuscript.
References
Footnotes
-
Contributors PJM-vdM and KGS contributed to the conception of this paper, critically read and modified subsequent drafts and approved the final version. PJM-vdM collected and analysed the data and wrote the first draft. The authors are both editors at BMJ Quality & Safety.
-
Competing interests None.
-
Provenance and peer review Not commissioned; internally peer reviewed.